1. Suatu sistem pegas bermassa digantungkan pada atap sebuah kereta. Pada awalnya kereta dalam keadaan diam dan diketahui bahwa pegas menyimpang sejauh 4 cm dari panjang rileksnya. Kemudian kereta dipercepat secara horizontal dengan percepatan sebesar a = ¾ g dengan g percepatan gravitasi, sehingga sistem pegas tersebut menjadi miring dan simpangannya bertambah besar. Besar simpangan pegas baru jika diasumsikan massa tidak bergerak terhadap kereta adalah ... cm.
2. Suatu bandul matematis dengan massa m dan panjang l digantungkan di atap sebuah kereta yang berada pada rel dengan kemiringan 60° terhadap horizontal. Saat kereta diam terhadap tanah karena direm, perioda bandul adalah T, namun saat rem dilepaskan dan kereta meluncur, perioda bandul berubah menjadi T′. Jika massa kereta jauh lebih besar daripada massa bandul, maka perbandingan T′/T adalah ...
3. Dua bola identik dilepaskan dari ketinggian yang sama namun bola pertama diberikan kecepatan horizontal awal sebesar sedangkan bola kedua tidak. Diketahui bahwa bola pertama mengenai batu setinggi 5 m yang berada pada jarak d dari titik awal, sedangkan bola kedua terdengar mengenai tanah beberapa saat kemudian. Jika diketahui bahwa gd²/v² = 20 m, maka ketinggian awal bola kedua adalah … m.
4. Dua bola diluncurkan dari permukaan tanah dengan kecepatan yang saling tegak lurus dengan laju masing-masingnya adalah v1 = 2 m/s, dan v2= 2√3 m/s, dan diketahui pula bahwa sudut peluncuran bola pertama terhadap tanah adalah 30°. Jika diketahui bahwa percepatan gravitasi adalah 10 m/s², maka lama waktu yang dibutuhkan hingga kecepatan kedua bola tegak lurus kembali adalah … s.
5. Suatu partikel sedang bergerak dalam lintasan parabola dalam pengaruh gravitasi dengan hambatan udara diabaikan. Apabila pada saat partikel memiliki besar komponen kecepatan vertikal 9 m/s dengan sudut kecepatan terhadap sumbu horizontal adalah 60°, maka besar komponen kecepatan arah vertikal pada saat sudut kecepatan terhadap sumbu horizontalnya 30° adalah ... m/s.
6. Tinjaulah sebuah balok diam bermassa 10 kg. Kemudian balok tersebut didorong dengan gaya sebesar 200 N, tetapi balok tersebut tetap diam. Jika diketahui lantai kasar dengan koefisien gesek statis μs , maka pada sistem tersebut gaya geseknya sama dengan …. N.
7. Suatu partikel bergerak menuruni bidang miring licin dari ketinggian R kemudian melewati suatu permukaan kasar datar dengan koefisien gesek kinetik 0,5 dengan panjang L. Diujung permukaan kasar terdapat lintasan setengah lingkaran licin berjejari R. Apabila partikel lepas kontak pada sudut θ dengan nilai cos θ = ⅓, maka perbandingan panjang permukaan kasar terhadap jejari lingkaran adalah ...

8. Sebuah balok bermassa 2 kg yang awalnya diam ditarik oleh gaya F sebesar 12 N dan membentuk sudut \( \theta \) hingga bergerak seperti pada gambar dibawah ini.

9. Sebuah proyektil ditembakkan dari permukaan tanah ke udara dengan kecepatan awal tertentu dan sudut elevasi \( \alpha \) terhadap horisontal. Percepatan gravitasi g ke bawah. Hambatan udara dapat diabaikan. Jika tinggi maksimum proyektil sama dengan h, sedangkan jangkauan mendatar maksimum sama dengan R, maka terdapat hubungan
\[ tan \alpha = n\frac{h}{R} \]
dengan nilai n sama dengan .....
10. Mobil A berada 25 km di depan mobil B. Mula-mula mobil A bergerak maju meninggalkan mobil B dengan kecepatan awal 30 km/jam dan percepatan konstan 2 km/jam². Satu jam kemudian mobil B mulai bergerak menyusul mobil A dengan kecepatan awal 40 km/jam dan percepatan konstan 5 km/jam². Ketika mobil B tepat menyusul mobil A, kecepatan mobil B sama dengan ..... km/jam.
11. Seorang anak (m = 20 kg) duduk diatas sebuah meja datar yang dapat diputar. Meja kemudian diputar dengan kecepatan sudut sebesar 2 rad/detik. Jika koefisien gesek si anak terhadap meja 0,4, maka jarak maksimum yang ditempuh secara radial oleh si anak diatas meja tanpa slip adalah ... cm.
12. Seseorang bermassa 80 kg melompat dari ketinggian 1 meter dan ia lupa menekuk lututnya pada saat mendarat. Tubuhnya mengalami perlambatan pada jarak satu cm. Gaya total yang ia rasakan pada kakinya selama perlambatan adalah ... N.
13. Sebuah partikel telah berpindah sepanjang lintasan pada bidang xy dari titik 1 yang vektor jari-jarinya \( \vec{r_1} = \hat{i} + 2\hat{j} \) ke titik 2 dengan vektor jari-jarinya \( \vec{r_2} = 2\hat{i} - 3\hat{j} \) . Selama waktu itu partikel tersebut mengalami gaya \( \vec{F} = 3\hat{i} + 4\hat{j}\) . Jika \( \vec{r_1} \), \( \vec{r_2} \) dan \( \vec{F} \) dalam satuan SI, usaha yang dilakukan oleh gaya F adalah ... Joule.
14. Sebuah kendaraan melintasi jalanan berbentuk setengah lingkaran berjari-jari R = 160 cm selama 10 detik. Jika gaya gesek udara diabaikan, maka kecepatan rata-rata kendaran selama menempuh lintasan itu adalah ... cm/s.
15. Sebuah silinder A berada diatas bidang miring balok B seperti ditunjukkan pada gambar.

16. Tinjaulah sebuah balok bermassa 5 kg yang sedang bergerak dengan kecepatan 10 m/s, kemudian didorong oleh gaya sebesar 100 N. Jika diketahui lantai licin, maka energi kinetik sistem 1 detik setelah didorong adalah …. Joule.
17. Tinjau suatu sistem silinder yang terhubung dengan dua pegas berikut.

18. Sebuah partikel bermassa \( m = 100 gr \) dilontarkan secara horizontal oleh sebuah pegas berkonstanta \( k = 100 N/m \) dari pinggir sebuah tebing yang memiliki ketinggian \( h = 5 m \) dari permukaan laut. Benda mulanya ditekan ke arah pegas sejauh \( x = 20 cm \), kemudian dilepaskan. Terdapat tebing lain dengan ketinggian yang sama berjarak \( d = 3 m \) dari tebing pertama. Jika tiap tumbukan dianggap elastis, partikel akan memantul sebanyak … kali sebelum sampai ke permukaan laut.

19. Suatu sistem satu dimensi memiliki energi potensial U (bersatuan Joule) sebagai fungsi jarak x (bersatuan meter) yang dinyatakan dalam bentuk
\[ U(x) = 3x^2 - 4x^3 \]
Jika \( x_0 \) adalah posisi kesetimbangan stabil sistem, maka nilai \( U(x_0 - 1) \) sama dengan ..... Joule.
20. Tinjau sebuah kubus dengan sisi R. Kemudian 7 buah massa identik m ditempatkan pada titik sudut kubus sehingga menyisakan satu titik kubus yang tidak berisi massa. Jika energi potensial gravitasi sistem tersebut dapat dituliskan dalam bentuk
\[ U_{grav} = -\frac{Gm^2}{R} \left [a + \frac{b}{\sqrt{2}} + \frac{c}{\sqrt{2}} \right] \]
maka nilai \( a + b + c \) = .....
21. Sebuah partikel bergerak sepanjang sumbu x dengan percepatan yang dapat dituliskan sebagai \( a = 6t - 2 \) m/s². Mula-mula partikel tersebut berada pada posisi x = 40 m dengan kecepatan awal 8 m/s ke arah x negatif. Ketika partikel tersebut berada pada keadaan diam untuk \( t \gt 0 \), posisi partikel tersebut berada di x = ..... m.
22. Sebuah batu jatuh bebas dari ketinggian \( H \) dan menumbuk bidang miring bersudut \( 45^{\circ} \) pada titik yang tingginya \( h \). Akibat tumbukan ini, batu bergerak dengan kecepatan mendatar. Agar total waktu yang diperlukan batu untuk mencapai tanah bersifat maksimum, maka nilai \( H/h \) sama dengan .....
23. Sebuah batu bata (m = 0,5 kg) yang sedang bergerak dengan kecepatan 5 m/s mulai mendaki suatu bidang miring dengan kemiringan \( \theta = 30^{\circ} \) terhadap bidang horizontal. Jika koefisien gesek batu bata terhadap bidang miring \( \mu = \sqrt{3}/12 \) , maka posisi batu bata terhadap posisi awal di bidang miring setelah ia mendaki selama 1,3 detik adalah … m.
24. Sebuah mobil dengan massa 1200 kg yang sedang melaju dengan kecepatan 60 km/jam di jalan datar tiba-tiba dimasukkan ke gigi netral (yaitu dibiarkan meluncur), sehinga kecepatannya berkurang dengan cara: \( v = \frac{v_0}{1 + (t/60)} \) km/jam, dimana t dalam detik. Daya yang diperlukan untuk mengendarai mobil ini dengan kecepatan 30 km/jam di jalan yang sama adalah … kWatt
25. Tinjau sistim silinder-balok sebagaimana terlihat pada gambar. Diketahui massa silinder A, \( m_A \) = 1,2 kg, dan balok B, \( m_B \) = 1 kg. Gaya gesek antar permukaan silinder-balok maupun balok-lantai diabaikan. Jika sudut kemiringan balok \( \alpha = 30^{\circ} \), maka besarnya percepatan balok B … m/s².

26. Sebuah pesawat sedang melakukan manuver dengan berputar pada trak lingkaran vertikal berjari-jari R = 500 m dengan kecepatan konstan v = 360 km per jam. Jika massa pilot m = 70 kg, maka berat pilot minimum yang akan terukur adalah … N
27. Sebuah mobil bergerak dengan percepatan tangensial konstan at = 0,62 m/s² sepanjang lintasan lingkaran datar berjejari R = 40 m. Koefisien gesek antara roda mobil dan permukaan jalan \( \mu \) = 0,20. Jika mobil mulai bergerak dari keadaan diam, maka jarak maksimum yang dapat ditempuh mobil untuk melaju tanpa tergelincir adalah … m.
28. Sebuah perahu motor bermassa m = 200 kg bergerak menyusuri danau dengan kecepatan \( v_0 \) = 72 km/jam. Pada saat t = 0 mesin perahu dimatikan. Dengan asumsi hambatan udara diabaikan, dan hambatan air sebanding dengan kecepatan perahu \( F = -kv \) (nilai k = 4 N.s.m-1), maka total jarak yang ditempuh perahu sejak mesin dimatikan hingga berhenti adalah … m.
29. Gabungan antara gesekan udara dan hambatan udara pada seorang pengendara sepeda menghasilkan gaya sebesar \( F = aV \), dengan \( V \) adalah kecepatannya dan a = 3 Newton-detik/m. Jika dengan tenaga maksimal, pengendara sepeda mampu menghasilkan daya penggerak sebesar 600 Watt, maka kecepatan maksimumnya di permukaan datar yang tidak ada angin adalah ... m/s.
30. Suatu sistem terdiri dari dua pegas yang dihubungkan secara seri dan mempunyai konstanta pegas \( k_1 \) = 3,2 N/m dan \( k_2 \) = 4,5 N/m. Usaha minimum yang harus dilakukan untuk meregangkan sistem ini sejauh s = 2,5 cm adalah ... mJ.
31. Sebuah partikel dilemparkan di dalam bangunan berbentuk trapesium dengan panjang sisi masing-masing \( s \), \( 2s \), \( 2s \), dan \( 3s \) seperti pada gambar (nilai \( s \) = 1 m). Partikel dilemparkan pada sisi kiri dan diinginkan dapat mengenai titik di sisi kanan pada ketinggian yang sama dengan titik pelemparan, dengan menyinggung sisi atas bangunan. Diketahui percepatan gravitasi sebesar \( g \) dan kecepatan awal pelemparan partikel sebesar \( v_0 = \sqrt{\frac{23 \sqrt{3} gs}{6}} \). Maka agar hal tersebut dapat terjadi, partikel harus dilempar pada jarak … m dari titik sudut kiri bawah bangunan.

32. Terdapat sistem tiga silinder yang saling tidak slip satu sama lain seperti terlihat pada gambar. Silinder A dan B hanya dapat berotasi terhadap titik pusatnya dengan kecepatan sudut konstan masing-masing \( \omega_A = 5 rad/s \) dan \( \omega_B = 4 rad/s \), sedangkan C dapat berotasi serta berevolusi. Jika diketahui jari-jari silinder A dan B masing-masing adalah\( r_A = 5 cm \) dan \( r_B = 13 cm \), maka kecepatan sudut revolusi silinder C adalah … rad/s

33. Dua buah balok identik bermassa \( m_b = 2 Kg \) diletakkan di atas papan panjang bermassa \( m_p = 4 Kg \) yang akan ditarik dengan gaya F. Koefisien gesek statik antara balok 1 dan 2 dengan papan masing-masing adalah \( \mu_{s1} \) = 0,8 dan \( \mu_{s2} = \frac{1}{2} \mu_{s2} \), sedangkan koefisien gesek kinetiknya sama sebesar \( \mu_k \) = 0,3. Agar kedua balok dapat bertumbukan, dan jika F minimum dan maksimum masing-masing bernilai p dan q, maka p + q adalah .... N

34. Sebuah batang dengan panjang L = 4 m bermassa \( m_1 \) = 1 Kg diletakkan di atas dua silinder pejal identik berjari-jari r = 80 cm dengan massa total \( m_2 \) = 2 Kg. Sistem tersebut mula-mula diam dan berada di atas bidang miring dengan sudut \( \theta \) = 30°. Posisi kedua silinder hampir saling bersentuhan dan awalnya ujung bawah batang tepat ada di atas silinder depan. Jika permukaannya sangat kasar sehingga gaya-gaya gesek kedua silinder sama, maka waktu yang dibutuhkan agar ujung atas batang menyentuh silinder belakang adalah … 𝑠

35. Sebuah bandul terdiri dari tali tak bermassa yang di ujungnya diberi massa, mula-mula memiliki sudut sebesar 45° terhadap vertikal. Percepatan gravitasi sebesar g ke bawah. Setelah dilepas tanpa kecepatan awal, nilai minimum dari percepatan total massa tersebut adalah a dengan g/a = n. Nilai n² sama dengan .....
36. Setetes air hujan jatuh vertikal dalam suatu kabut, sehingga massanya bertambah. Titik air hujan tersebut tetap berbentuk bola, dimana laju pertambahan massanya sebanding dengan kecepatan dan kuadrat jari-jarinya. Tetes air hujan tersebut mulamula jatuh tanpa kecepatan awal dengan ukuran jari-jari yang dapat diabaikan. Anggap rapat massa air hujan selalu tetap, dan percepatan gravitasi \( g \) ke bawah. Jika percepatan titik air hujan tersebut sama dengan \( a \) maka \( g/a \) sama dengan …
37. Dua balok bermassa ml = 1,3 kg dan m2 = 2,5 kg dihubungkan oleh pegas tanpa massa dengan k = 13 N/m (lihat gambar) berada pada bidang horizontal yang licin. Balok 2 ditekan ke kiri sejauh x = 5 cm kemudian dilepaskan. Kecepatan pusat massa sistem setelah balok 1 lepas dari dinding adalah … cm/s.

38. Sebuah bola yang bergerak secara translasi bertumbukan elastik dengan bola lain yang sedang diam dan bermassa sama. Pada saat tumbukan, sudut antara garis lurus yang melalui titik pusat bola dan arah gerak awal bola yang dipukul adalah \( \alpha \) = 45°. Dengan asumsi bola licin, prosentase energi kinetik bola yang dipukul yang berubah menjadi energi potensial pada saat deformasi maksimum adalah … %
39. Sebuah batang tipis homogen AB bermassa m = 1.0 kg bergerak translasi dengan percepatan \( a \) = 2.0 m/s² akibat dua gaya yang saling berlawanan \( F_1 \) dan \( F_2 \) (lihat gambar). Jarak antara titik-titik di mana gaya-gaya ini diterapkan adalah \( b \) = 20 cm. Jika diketahui \( F_2 \) = 5,0 N maka panjang batang tersebut … m.

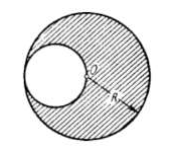
40. Sebuah piringan homogen berjari-jari R = 20 cm mempunyai lubang lingkaran seperti ditunjukkan pada gambar. Massa bagian piringan yang tersisa (yang diarsir) m = 7,3 kg. Momen inersia piringan tersebut terhadap sumbu yang melalui pusat massanya dan tegak lurus terhadap bidang piringan adalah …. kg.m².
Komentar
Posting Komentar